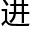
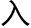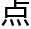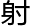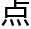这个空间的另一段只要最近的平行空间然后顺着那另外的空间上相对的一回到自己的空间就可以了。不过因为自己在另一个空间有着影的那一所以要想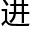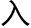并存活下来只能消灭自己

空间。但在量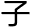理学不确定因素的影响下这些平行空间也可能是不稳定的如果由这些不确定的普朗克常量构成的平行空间就存在消亡的可能。

何维度来看这个都不备方向与长度所以它没有维度只能用o来表示也就是所谓的原。同理比它低级的空间是不存在的。所以零维空间只能投影到更级的空间。

有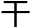预空间的投影。不过在更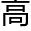维度的空间里这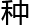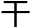预就会变得最小这时只有两条互相平行的空间互相的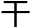预才是最大的（因为互相都有在彼此空间的投影）。而如果其中一个空间想要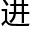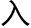自己

可能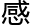知对方更不可能相撞。

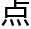
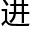
还要注意的就是空间延伸的度问题。例如两个平行的平行空间他们延伸的率是不同的其中贝它空间比阿尔空间的延伸率要快。那么当从阿尔空间上的一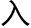贝它空间后向前移动

那么它就都可以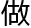到了因为它可以从外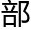随意选择这个空间的一段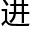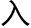。但是如果想这样它就必须备一个前提条件那就是变成二维空间中的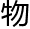因为二维空间要比它多一个维度作为一维空间

两个空间都是存在于更的维度之上的所以它们已经构成了二维空间的架构而这两个一维空间就是彼此的平行空间了。我们可以称这平行空间为预型平行空间（以下简称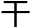平）。

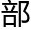
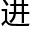
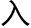到一维世界只有两个方法：增加维度和空间投影。

有一个普朗克常量不是我们所认知的普朗克常量的世界存在。比如用“1”来表示我们所知世界的普朗克常量的数值即“普朗克常数”如果另一个世界的普朗

增加维度就是制造空间。例如一条直线上有一个线段想要直接到这条直线上的另外一那么它可以在这个二维空间中创造一个新的一维空间来连接到原来空间中的某一从而通过这个空间达

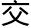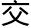
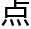
而空间投影则是另外一方法。大家都知二维空间中包了无数的一维空间而其中的两个一维空间平行或者相了（平行的可能只能有一）。相的两条线在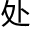产生了一个而这

了一些或

所以他们相遇时会毫无阻碍的穿过对方队列即不可能知对方更不可能相撞。同样普朗克常量不一样的两个世界就如一排奇数和一排偶数是能量最小单位的不一样把我们分在了两个空间不

中单独的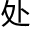二维空间（x轴、y轴）中它只是维度“宽”无限接近于零的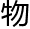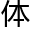而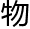理常识告诉我们无限接近于零的存在可以完全忽略所以它是不会存在的。所以它要想存在于二维空间或从外

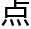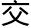个则从这里同时沿着两个空间延伸去。在延伸去的两个空间里又有无数的空间相了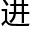来所以造成了无数的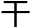平。而那些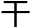平也被更多的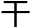平所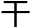预。这样一来所有的空间都会留下其余所

觉不到他们如果位置重叠我们和他们相遇而看不到对方会不会撞在一起呢？答案是否定的。最能直接表示两者之间关系的例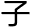就是奇数与偶数。奇数与偶数之间不会有永远这样平行存在着

虽然理论上这样的时空可以生成无穷多个但并不能真的像奇数与偶数一样可以从中取多个值。通过解普朗克常量方程科学家们只能得方程的几个合理的解由此可以构造几个可能存在的平行

在那个空间上的影否则就只能用第一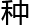方法另外制造一个空间了。

克常数的取值是“2”那么另一个世界就是建立在普朗克常数为“2”的基础之上。而从1到2之间又有无数个可取的值因此可能平行存在的世界也就应该是无穷无尽。可是我们为什么看不到他们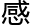

先由最简单的零维开始。所谓的维度用来衡量空间的一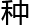矢量单位（有方向的单位）例如一维空间的维度是“x”二维空间的维度是“x、y”以此类推。因为零维空间只有一个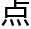无论从任

到跃的目的。如果它想创造一个二维空间的话就必须增加维度也就是所谓的制造异次元空间。它可以从原来的空间中的某一分一个新的空间看上去好像两个都属于一维空间；但是因为这

下面开始讲一维空间。一维空间的方向有一个如果用几何学表示可以写成x轴。如果一维空间中的想直接来到自己空间中的某一而不经过其他线段那么它只要突破了一维而来到二维