“既然他是叫别人来理自己的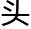 发的。”梦儿笑
发的。”梦儿笑 。“那么他的理发对象就已然受到限制,他不能把自己当
。“那么他的理发对象就已然受到限制,他不能把自己当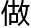 理发对象,他的
理发对象,他的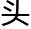 发已经被理了。第二条的限制依然奏效,即便是以间接的方式。”小西一听,恍然大悟,暗怪自己先前竟然未能察觉这
发已经被理了。第二条的限制依然奏效,即便是以间接的方式。”小西一听,恍然大悟,暗怪自己先前竟然未能察觉这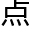 。
。
儒尊 :“继续。”
:“继续。”
“可惜,即便如此,也不妨碍我解开这一系列悖论。”梦儿 “这光之门上边的悖论是有限的,我可以一一拆解。”顿了顿,自顾解析
“这光之门上边的悖论是有限的,我可以一一拆解。”顿了顿,自顾解析 :“说谎者悖论,其实质是在直接确定‘我的话语’与‘谎话’的联系,这个联系是在‘
:“说谎者悖论,其实质是在直接确定‘我的话语’与‘谎话’的联系,这个联系是在‘ 备说话能力的主
备说话能力的主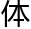 ’与‘谎话’这两条独立集合被确定的前提下才能建立的。而‘谎话’的定义是以‘所言之话语是否附和实际情况’来确认的,并非由‘
’与‘谎话’这两条独立集合被确定的前提下才能建立的。而‘谎话’的定义是以‘所言之话语是否附和实际情况’来确认的,并非由‘ 备说话能力的主
备说话能力的主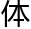 ’直接确定,所以这句话无效。我们可以把任意无效的、即无法确定其元素的集合定义为其元素为空集的集合。这样的话,就没有无法确定的集合,因为所有无法确定的集合都被归到一个特异的集合中。保全了集合论的完备
’直接确定,所以这句话无效。我们可以把任意无效的、即无法确定其元素的集合定义为其元素为空集的集合。这样的话,就没有无法确定的集合,因为所有无法确定的集合都被归到一个特异的集合中。保全了集合论的完备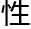 。”
。”
“好。”几番被驳,梦儿竟大声叫好,继而毫不气馁地 :“你这样说,确实能使罗素摆脱第二条信息的限制,但未必能摆脱所有限制。他的理发对象是由不自己理发的人所组成的集合中划分过来的,这个你认同否?”
:“你这样说,确实能使罗素摆脱第二条信息的限制,但未必能摆脱所有限制。他的理发对象是由不自己理发的人所组成的集合中划分过来的,这个你认同否?”
“上述所言的集合全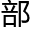 都是基于第二条信息得以划分的,而第三条信息透
都是基于第二条信息得以划分的,而第三条信息透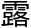 的,是指罗素可以从上述集合中任选其一或者以上来作为自己的理发对象,这便是他的权力。不过,显然,他扩大了自己的权力,他给
的,是指罗素可以从上述集合中任选其一或者以上来作为自己的理发对象,这便是他的权力。不过,显然,他扩大了自己的权力,他给 的理发条件竟无视第二条信息。所以应当废除或改
的理发条件竟无视第二条信息。所以应当废除或改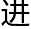 。”
。”
儒尊即刻抢断 :“若你是仿效先前那位神官,指明判断主
:“若你是仿效先前那位神官,指明判断主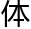 不可判断自
不可判断自 ,那么,你自己便已陷
,那么,你自己便已陷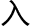 悖论,因为你的判断原则同样既是判断主
悖论,因为你的判断原则同样既是判断主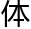 又是判断对象。正如他所谓的分层原则既是分层主
又是判断对象。正如他所谓的分层原则既是分层主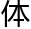 又是分层对象一般。”
又是分层对象一般。”
儒尊淡漠 :“这个我自然承认。把他的理发对象看
:“这个我自然承认。把他的理发对象看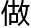 是一个集合的话,那么这个集合就是不自己理发的人所组成的集合的
是一个集合的话,那么这个集合就是不自己理发的人所组成的集合的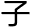 集。”
集。”
“既然可以同时确定,那么可见两个集合的确定次序可以互换。”儒尊 。
。
“还是不对。”儒尊又反驳 “先前你已表明,允许
“先前你已表明,允许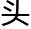 发先别人理再自己理,那么罗素的
发先别人理再自己理,那么罗素的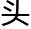 发被别人理了以后,他又要自己理了呢?悖论依然会存在。而且完全摆脱第二条的限制,罗素的
发被别人理了以后,他又要自己理了呢?悖论依然会存在。而且完全摆脱第二条的限制,罗素的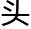 发是在理过之后再讨论他自己该理与否的。”小西再次恍悟,暗叹儒尊果真大智,三言两语之下竟又颠倒乾坤,他不由又暗责自己太容易陷
发是在理过之后再讨论他自己该理与否的。”小西再次恍悟,暗叹儒尊果真大智,三言两语之下竟又颠倒乾坤,他不由又暗责自己太容易陷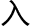 他人的逻辑框架中。其旁的剑景却听得浑浑噩噩。
他人的逻辑框架中。其旁的剑景却听得浑浑噩噩。
儒尊 :“正是如此。则又如何?”
:“正是如此。则又如何?”
“没错,其实还可以用另一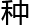 角度解决它。”梦儿阐述
角度解决它。”梦儿阐述 “从理发师悖论中我们可以获取一下信息:第一,罗素是本城镇的人;第二,这个城镇的居民的
“从理发师悖论中我们可以获取一下信息:第一,罗素是本城镇的人;第二,这个城镇的居民的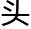 发必须有人理;第三,罗素在一定程度上有决定自己理发对象的权力。”
发必须有人理;第三,罗素在一定程度上有决定自己理发对象的权力。”
梦儿笑 :“既然时空可逆转,过去、现在与未来便没有区别,它们都是时空片
:“既然时空可逆转,过去、现在与未来便没有区别,它们都是时空片
“嘿。”梦儿轻笑一声,论述 :“既然罗素的理发对象是在另一个集合内划分
:“既然罗素的理发对象是在另一个集合内划分 来的,那么定然受到这个集合的限制。他的理发对象不可能超
来的,那么定然受到这个集合的限制。他的理发对象不可能超 这个集合的元素范围。比如,某个人既然自己替自己理发了,罗素定然不能为他理发,对不?”
这个集合的元素范围。比如,某个人既然自己替自己理发了,罗素定然不能为他理发,对不?”
梦儿 :“则恰好说明,在不自己理发的人组建的集合未确定之前,罗素的理发对象是无法确定的。罗素的理发对象必须比前一个集合后一步确定或者同时确定,这就是限制。”
:“则恰好说明,在不自己理发的人组建的集合未确定之前,罗素的理发对象是无法确定的。罗素的理发对象必须比前一个集合后一步确定或者同时确定,这就是限制。”
“首先,时空是可逆转的,这是那 悖论的前提。”梦儿
悖论的前提。”梦儿 “如果时空不可逆转,那么就无所谓的回到过去。对否?”
“如果时空不可逆转,那么就无所谓的回到过去。对否?”
儒尊默然不答,梦儿继续论述 :“不
:“不 是‘世事无绝对’或者‘没有立场的立场’,还是‘怀疑一切’及其他一切悖论,莫不是错误地建立一
是‘世事无绝对’或者‘没有立场的立场’,还是‘怀疑一切’及其他一切悖论,莫不是错误地建立一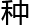 联系,一
联系,一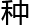 违背两个被联系的对象范畴的联系,这类联系叫无效联系。仅此而已。”
违背两个被联系的对象范畴的联系,这类联系叫无效联系。仅此而已。”
儒尊轻哼一声,说 :“你这与寻求绝对的原因,不需要原因的原因。一样的无稽。”
:“你这与寻求绝对的原因,不需要原因的原因。一样的无稽。”
论的立场来添补漏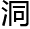 ,而不是一味地在悖论里绕圈。”
,而不是一味地在悖论里绕圈。”
“那时间悖论呢?”儒尊说 “它没有
“它没有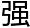 行地建立无效联系吧?”
行地建立无效联系吧?”
儒尊驳 :“我以为不然,罗素的
:“我以为不然,罗素的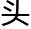 发可以叫别人来理,那他的理发对象就不受第二条的限制,因为该城镇的人都能得以理发。”
发可以叫别人来理,那他的理发对象就不受第二条的限制,因为该城镇的人都能得以理发。”
“试着便知。”梦儿不急不恼地说“现在是说谎者悖论,‘我在说谎’或者‘这句话是错的’这两句都将导致悖论的 现,因为它们既是判断主
现,因为它们既是判断主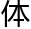 又是判断对象。”
又是判断对象。”
“非也。”梦儿学着儒尊先前的腔调否定 “这两个集合的关系跟因果关系相似,在大逻辑框架内没有赋予因果次序逆转的自由度,那么便不可逆转。刚才我已经指明了限制,则不可逆转次序。”
“这两个集合的关系跟因果关系相似,在大逻辑框架内没有赋予因果次序逆转的自由度,那么便不可逆转。刚才我已经指明了限制,则不可逆转次序。”
“由于该城镇的居民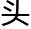 发必须有人理,那么必然可以划分
发必须有人理,那么必然可以划分 一些集合。比如,
一些集合。比如,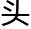 发自己理的人是一个集合,
发自己理的人是一个集合,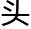 发被别人理的人能组成一个集合,
发被别人理的人能组成一个集合,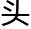 发先是自己理而后又给别人理的又是一个集合,
发先是自己理而后又给别人理的又是一个集合,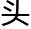 发先是别人理再而自己理的人又可以组成一个集合等。”
发先是别人理再而自己理的人又可以组成一个集合等。”
“那假若,我寻得一个终极原则,该原则是唯一既是主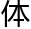 又是对象的命题并且有效,便可以指明其他任意悖论。”梦儿
又是对象的命题并且有效,便可以指明其他任意悖论。”梦儿 。
。
儒尊略微思索,暗觉梦儿此法居然尚可,一时间她也无法寻找漏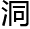 ,先前以为已将其致命弊端指
,先前以为已将其致命弊端指 ,未想她竟能起死回生,罢了,先承认一次又有和不可。一念及此,儒尊
,未想她竟能起死回生,罢了,先承认一次又有和不可。一念及此,儒尊 声
声 :“也罢,我姑且承认理发师悖论在你指明的限制下可以消解,但这悖论可是成一系列的,若你不能将所有限制归纳统一,而是一一指明,恐怕也算不得真正解决悖论的存在。”
:“也罢,我姑且承认理发师悖论在你指明的限制下可以消解,但这悖论可是成一系列的,若你不能将所有限制归纳统一,而是一一指明,恐怕也算不得真正解决悖论的存在。”