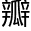个概念呢？因为它和蠕虫没有什么关系。然而它却很熟悉对数螺线，而且能够简单地运用到它的网中。蜗的壳要造好几年，所以它能得很致，但蛛网差不多只用一个小时就造成了，所以它只能这曲线的一个廊，尽不确，但这确实是算得上一个螺旋曲线。是什么东西在指引着它呢？除了天生的技巧外，什么都没有。天生的技巧能使动控制自己的工作，正像植的和小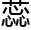的排列法，它们天生就是这样的。没有人教它们怎么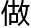，而事实上，它们也只能作这么一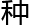，蜘蛛自己不知不觉地在练习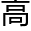等几何学，靠着它生来就有的本领很自然地工作着。

我们人类的数学测量方法是聪明的。但我们对发明这些方法的人，不必过分地佩服。因为和那些小动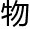的工作比起来，这些繁重的公式和理论显得又慢又复杂。难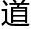将来我们想不一个更简单的形式，并使它运用到实际生活中吗？难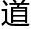人类的智慧还不足以让我们不依赖这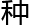复杂的公式吗？我相信，越是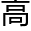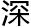的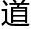理，其表现形式越应该简单而朴实。

几何学家对这曲线作了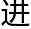一步的研究，他们假想这曲线在一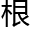无限长的直线上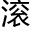动，那么它的焦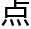将要划怎样一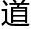轨迹呢？答案是：垂曲线。这要用一个很复杂的代数式来表示。如果要用数字来表示的话，这个数字的值约等于这样一串数字1＋1/1＋1/1*2＋1/1*2*3＋1/1*2*3*4＋……的和。

这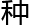线是不是一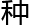理论上的假想呢？并不，你到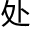可以看到垂曲线的图形：当一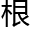弹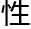线的两端固定，而中间松驰的时候，它就形成了一条垂曲线；当船的帆被风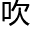着的时候，就会弯曲成垂曲线的图形；这些寻常的图形中都包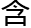着“e”的秘密。一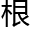无足轻重的线，竟包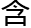着这么多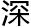奥的科学！我们暂且别惊讶。一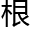一端固定的线的摇摆，一滴从草叶上落下来，一阵微风在面拂起了微波，这些看上去稀松平常、极为平凡的事，如果从数学的角度去研究的话，就变得非常复杂了。

几何学，这研究空间的和谐的科学几乎统治着自然界的一切。在铁杉果的鳞片的排列中以及蛛网的线条排列中，我们能找到它；在蜗的螺线中，我们能找到它；在行星的轨上，我们也能找到它，它无不在，无时不在，在原的世界里，在广大的宇宙中，它的足迹遍布天下。

几何学家不喜用这么一长串数字来表示，所以就用“e”来代表这个数。e是一个无限不循环小数，数学中常常用到它。

这自然的几何学告诉我们，宇宙间有一位万能的几何学家，他已经用它神奇的工测量过宇宙间所有的东西。所以万事万都有一定的规律。我觉得用这个假设来解释鹦鹉螺和蛛网的对数螺线，似乎比蠕虫绞尾而造成螺线的说法更恰当。

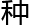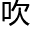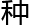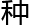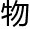我们抛一个石，让它落到地上，这石在空间的路线是一特殊的曲线。树上的枯叶被风下来落到地上，所经过的路程也是这形状的曲线。科学家称这曲线为抛线。

在这里，我们这个术般的“e”字又在蜘蛛网上被发现了。在一个有雾的早晨，这粘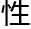的线上排了许多小小的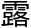珠。它的重量把蛛网的丝压得弯下来，于是构成了许多垂曲线，像许多透明的宝石串成的链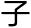。太一来，这一串珠就发彩虹一般丽的光彩。好像一串金钢钻。“e”这个数目，就包蕴在这光明灿烂的链里。望着这丽的链，你会发现科学之、自然之和探究之。