转向机由一张无限长且被分隔成一个个小方块的纸条和一个能左右移动或保持静止的打印/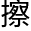 洗
洗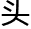 组成。打印/
组成。打印/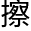 洗
洗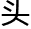 可以在小方块内打上个记号,或是将格内原有的记号抹去。通过给打印/
可以在小方块内打上个记号,或是将格内原有的记号抹去。通过给打印/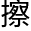 洗
洗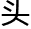 的运动和行为编程可以解决任何计算问题。我
的运动和行为编程可以解决任何计算问题。我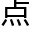
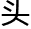 示意霍勒斯继续。
示意霍勒斯继续。
吕特人的 睛看到的是完整的周围全景,而且无需聚焦所有
睛看到的是完整的周围全景,而且无需聚焦所有
 一直都以同等清晰度被观察着。你们人类和我们弗林纳人使用诸如集中注意力或是聚焦之类表达方式来描述视觉和
一直都以同等清晰度被观察着。你们人类和我们弗林纳人使用诸如集中注意力或是聚焦之类表达方式来描述视觉和 神上的活动。例如你集中注意力在某个
神上的活动。例如你集中注意力在某个
 上,或是聚焦在某个问题上。吕特人不这么
上,或是聚焦在某个问题上。吕特人不这么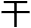 。他们同
。他们同
活到老,学到老。霍勒斯说,我们这一族一般最多可以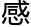 觉到六个
觉到六个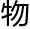
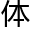 的数集比你们稍
的数集比你们稍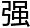 一
一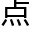 。但吕特人使我们大吃一惊,一个正常的吕特人可以
。但吕特人使我们大吃一惊,一个正常的吕特人可以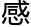 觉到多达四十六个单元的数集,一些个
觉到多达四十六个单元的数集,一些个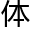 甚至能
甚至能 觉到六十九个。
觉到六十九个。
是的,但他们无法清晰地描述总数。他们真的没有这样的词汇。能够 觉更多数目的吕特人明显有竞争优势。他们中的某位可能会提
觉更多数目的吕特人明显有竞争优势。他们中的某位可能会提 用他的五十二只家畜去换别人的六十八
用他的五十二只家畜去换别人的六十八 ,而那个别人由于天分不
,而那个别人由于天分不 ,只知
,只知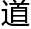 这两个都是很多的大数,却无从评估此次
这两个都是很多的大数,却无从评估此次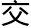 易是否公平。吕特人的僧侣几乎都有超过平均
易是否公平。吕特人的僧侣几乎都有超过平均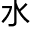 平的
平的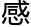 觉。
觉。
只有当你面对六个以上的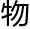
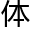 时,你才会开始数数。
时,你才会开始数数。
真是奇妙啊!我说。
但吕特人有二十三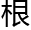 手指,二十三是个质数。除了一和二十三以外,它没有其他能被整除的数,而二十三这个除数又太大了,在现实生活中没有什么实际应用价值。它也不是任何连续的自然数序列之和。二十一和二十八分别是
手指,二十三是个质数。除了一和二十三以外,它没有其他能被整除的数,而二十三这个除数又太大了,在现实生活中没有什么实际应用价值。它也不是任何连续的自然数序列之和。二十一和二十八分别是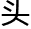 六个和
六个和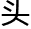 七个自然数之和。二十三却没有类似特
七个自然数之和。二十三却没有类似特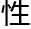 。由于他们的手指的分布形式,他们从未发展
。由于他们的手指的分布形式,他们从未发展 数数或是我们用的数学。
数数或是我们用的数学。
但你说有些个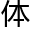 能
能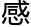 觉到更多的数目?
觉到更多的数目?
霍勒斯听懂了双关语。他的 柄起着波纹。
柄起着波纹。
但吕特人从未组成过成员超过二十一个他们能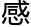 觉到的量名的永久
觉到的量名的永久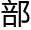 落。而且,如果在你左面有四十九个敌人,而在右面有五十个,这两个数之间没有本质的差别,无论走哪边你都死定了。他停顿了一下,用人类的话说,自然界对于吕特人留了一手或是留了四手。你有十
落。而且,如果在你左面有四十九个敌人,而在右面有五十个,这两个数之间没有本质的差别,无论走哪边你都死定了。他停顿了一下,用人类的话说,自然界对于吕特人留了一手或是留了四手。你有十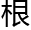 手指。十是个
手指。十是个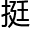 奇妙的数字,它本
奇妙的数字,它本 就会把人引
就会把人引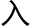 数学。它是个偶数,可以被二和五整除。它还是
数学。它是个偶数,可以被二和五整除。它还是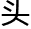 四个自然数的和:一加二加三加四等于十。我们弗林纳人运气也不错。我们依靠跺脚来数数,总共六只脚也是个偶数,可以被二和三整除。它也是
四个自然数的和:一加二加三加四等于十。我们弗林纳人运气也不错。我们依靠跺脚来数数,总共六只脚也是个偶数,可以被二和三整除。它也是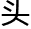 三个自然数的和:一加二加三等于六。又一个适于数学的意识基础。
三个自然数的和:一加二加三等于六。又一个适于数学的意识基础。
我在Discovery频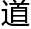 上看到过一个研究数数的节目。
上看到过一个研究数数的节目。
他有,而且只有一只那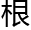 绕在他躯
绕在他躯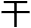
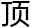 端的
端的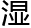 漉漉的黑条。那是个能从一圈360度同时观察的长
漉漉的黑条。那是个能从一圈360度同时观察的长 。一个令人着迷的结构:吕特人的视网
。一个令人着迷的结构:吕特人的视网 是由一层层光
是由一层层光 薄片组成的。这些薄片以错综复杂的顺序不断飞快地在透明和非透明之间转换。它们的薄片层层堆积,厚度超过一厘米,可以同时在不同的焦距下提供清晰图像。
薄片组成的。这些薄片以错综复杂的顺序不断飞快地在透明和非透明之间转换。它们的薄片层层堆积,厚度超过一厘米,可以同时在不同的焦距下提供清晰图像。
确实是。霍勒斯说,还有,你一定注意到了卡纳的 睛。
睛。
好吧,但这有什么意义吗?
真的吗?但当面对更多的
 时会发生什么?他们得从一开始把它们全数一遍吗?
时会发生什么?他们得从一开始把它们全数一遍吗?
外来的和尚好念经。我说。
在地球上, 睛已经
睛已经 化过很多次了。我说,昆虫、
化过很多次了。我说,昆虫、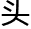 足类、脊椎动
足类、脊椎动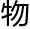 ,还有其他很多
,还有其他很多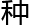 类都各自独立地发展
类都各自独立地发展 了视觉。但我从未听说过任何
了视觉。但我从未听说过任何 睛像那个样
睛像那个样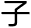 。
。
碰到吕特人之前我们也不知 。霍勒斯说,但他们
。霍勒斯说,但他们 睛的结构也影响了他们的思维。让我们再谈谈数学。考虑一下所有数字计算机的基本模型,不
睛的结构也影响了他们的思维。让我们再谈谈数学。考虑一下所有数字计算机的基本模型,不 它是地球人的还是弗林纳人的。
它是地球人的还是弗林纳人的。 据我在电
据我在电 公告板上看到的一个纪录片,你们称这
公告板上看到的一个纪录片,你们称这 模型为转向机?
模型为转向机?
为什么你会认为他们从来就没能够发展数数的能力呢?
不。吕特人不会数数。他们真的是不知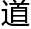 怎么数。他们要么能
怎么数。他们要么能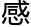 觉到整个数集,要么不能。他们对于从一到四十六的每个数都有单独的称呼,对于超过四十六的则简单地称为很多。
觉到整个数集,要么不能。他们对于从一到四十六的每个数都有单独的称呼,对于超过四十六的则简单地称为很多。
我们的大脑只拥有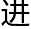 化给予的能力。对于你我的祖先来说,知
化给予的能力。对于你我的祖先来说,知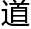 如何确定大于五的数目是一
如何确定大于五的数目是一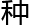
 有现实意义的生存优势:如果有七个愤怒的敌人挡住了你左边的去路,而在右边有八个,则你向左边走存活的机会要大一
有现实意义的生存优势:如果有七个愤怒的敌人挡住了你左边的去路,而在右边有八个,则你向左边走存活的机会要大一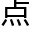 ,尽
,尽 不会大很多。如果你的
不会大很多。如果你的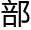 落包括你在内有十个人,而你的任务又是为晚餐采集野果,那么你最好能带回十份野果,否则你将会在
落包括你在内有十个人,而你的任务又是为晚餐采集野果,那么你最好能带回十份野果,否则你将会在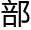 落里树敌。实际上,仅仅采集九份野果,更有可能的局面是你放弃你自己的那份以讨好你的同伴,结果就是,你的努力没有给你个人带来任何好
落里树敌。实际上,仅仅采集九份野果,更有可能的局面是你放弃你自己的那份以讨好你的同伴,结果就是,你的努力没有给你个人带来任何好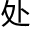 。
。
节目研究了人类数数有多快。如果给你看一个、两个、三个、四个或是五个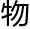
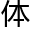 ,你可以在差不多的时间内回答有几个
,你可以在差不多的时间内回答有几个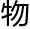
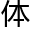 。只有当
。只有当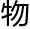
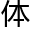 超过六个时,回答时间会延长,并且回答所需时间的延长与
超过六个时,回答时间会延长,并且回答所需时间的延长与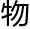
 增加的个数成正比。
增加的个数成正比。
我很奇怪。实际上,没有。他好像没有 睛。
睛。
我从未听说过。我说。
你怎么知 这些的?
这些的?